کامپیوترها هنوز در انجام کارهای هوشمندانه مشکلات بسیاری دارند،
اما اینکه از آنها بخواهیم محاسبات را انجام دهند که انتظار زیادی نیست، هست؟
برنامهنویسان به خوبی میدانند که گاهی ماشین حساب آنلاین گوگل و برنامه اکسل مایکروسافت حتی از پس محاسبات ساده هم برنمیآیند. اما به هر حال، مشکلات گاه و بیگاه آنها را نمیتوان اشکال دانست. در حقیقت، این مشکلات نشان نمیدهند که کامپیوترها در انجام کارهای ریاضی ناتوان هستند!
کامپیوترها محاسبات را به شیوه کاملا متفاوتی نسبت به انسانها انجام میدهند و اغلب هم به پاسخ نادرست میرسند. برای آنهایی که هنوز متقاعد نشدهاند که کامپیوترها قادر به انجام اعمال ساده ریاضی نیستند، با چند مثال شروع میکنیم.
مثلا ماشین حساب گوگل را در نظر بگیرید. برای استفاده از آن کافیست عبارت ریاضی مورد نظر را در کادر جستجوی گوگل تایپ کنید و آن را جستجو کنید تا نتیجه را ببینید، مثلا بنویسید ۵*۹+sqrt 9)^3) تا ببینید چه جوابی روی صفحه نمایش داده میشود. به طور حتم جواب درست است. اکنون محاسبه دیگری انجام میدهیم.
در کادر جستجوی گوگل عبارت زیر را تایپ کنید (شکل ۱):
۵۹۹,۹۹۹,۹۹۹,۹۹۹,۹۹۹ – ۵۹۹,۹۹۹,۹۹۹,۹۹۹,۹۹۸
مشخص است که پاسخ این عبارت ۱ است، اما گوگل اعتقاد دارد پاسخ این عبارت صفر میشود!
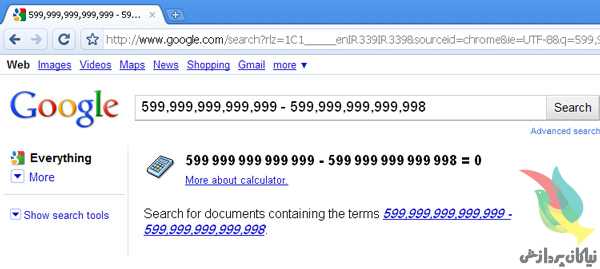
(شکل۱)
یا یک محاسبه ساده دیگر انجام دهیم. در یکی از سلولهای یک فایل اکسل ۲۰۰۷ عبارت زیر را بنویسید:
=۸۵۰*۷۷٫۱
اگر این روش کار نکرد (یعنی در واقع کار کرد!)، این کار را در نسخه قدیمیتری از اکسل انجام دهید تا ببینید که اکسل به جای پاسخ صحیح که ۶۵۵۳۵ است، عدد ۱۰۰۰۰۰ را نشان میدهد. البته این ایراد در برخی از نسخههای اکسل درست شده است.
به همین ترتیب، در ماشین حسابهای آنلاین (مانند http://calculator.net) عبارت زیر را محاسبه کنید:
۱٫۰ – ۰٫۹ – ۰٫۱
خواهید دید که به جای جواب صحیح که صفر است، با مقدار عجیب -۲٫۷۷۵۵۵۷۵۶ E-17 روبرو میشوید که نماد علمی عدد -۰٫۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۰۲۷۷۵۵۵۷۵۶ است (شکل ۲).
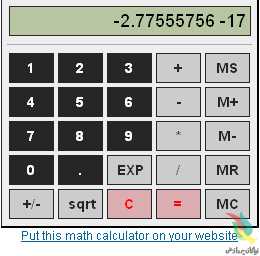
(شکل۲)
این جواب خیلی از صفر دور نیست اما چرا ماشین حساب پاسخ صحیح را نداد، پاسخی که به حدی روشن است که حتی فردی که حساب ساده را هم بلد نیست میتواند آن را به دست آورد؟
روش انجام محاسبات در کامپیوتر
با آنکه کامپیوترها میتوانند اعداد صحیح را نگه دارند، اما برای محاسبات عمومی ریاضی اعداد را در قالب ممیز شناور (Floating Point) ذخیره میکنند که روشی بسیار کارآمد در زمینه صرفهجویی در مصرف حافظه است.
مثلا نمایش ممیز شناور با دقت دوگانه، از ۶۴ بیت برای ذخیره هر عدد استفاده میکند و در آن میتوان اعداد از ۱۰۳۰۸- تا ۱۰۳۰۸ (یعنی منفی و مثبت یک با ۳۰۸ صفر در مقابلش) را ذخیره کرد. همچنین اعداد کسری حتی به کوچکی ۳۰۸-۱۰ (صفر، ممیز، ۳۰۷ صفر و سپس ۱) هم قابل ذخیرهسازی هستند.
به همین ترتیب اگر از همین ۶۴ بیت برای ذخیره اعداد صحیح استفاده شود، میتوان از اعداد ۹,۲۲۳,۳۷۲,۰۳۶,۸۵۴,۷۷۵,۸۰۸- تا ۹,۲۲۳,۳۷۲,۰۳۶,۸۵۴,۷۷۵,۸۰۷+ را البته بدون قسمت اعشاری در آن نگه داشت.
اما چگونه این حجم انبوه از اعداد در تنها ۶۴ بیت جا میگیرند؟ پاسخ این است: تقریب! از آن ۶۴ بیت، یکی برای نمایش علامت به کار میرود که نشان دهد عدد مثبت است یا منفی. ۵۲ بیت برای مانتیس (خود عدد) استفاده میشوند و ۱۱ بیت دیگر توان را نشان میدهند (یعنی اینکه چند صفر باید گذاشته شود و ممیز هم کجای عدد قرار میگیرد).
با آنکه طیف گستردهای از اعداد را میتوان به شیوه ممیز شناور نشان داد، اما دقت در عمل کمتر از قالب اعداد صحیح است چون تنها ۵۲ بیت برای این کار در نظر گرفته شده است. در عمل، ۵۲ بیت باینری تنها قادر به نشان دادن یک عدد ۱۶ رقمی مبنای ده است و اعدادی که رقم ۱۷ام آنها با هم فرق دارند، از دید کامپیوتر معادل در نظر گرفته میشوند.
به همین دلیل است که گوگل مقدار ۵۹۹,۹۹۹,۹۹۹,۹۹۹,۹۹۹ – ۵۹۹,۹۹۹,۹۹۹,۹۹۹,۹۹۸ را صفر میداند؛ البته مشخص است که مانتیس ماشین حساب گوگل کمتر از ۵۲ بیت است.
اما چرا محاسبه ۰٫۱ – ۰٫۹ – ۱٫۰ برابر با صفر نمیشود؟ به نظر میرسد شاید این موضوع ربطی به محدودیت ۶۴ بیتی نداشته باشد، چون ما با اعداد کوچکی سر و کار داریم. اما این طور نیست.
کامپیوترها اعداد را در مبنای دو ذخیره میکنند. عدد ۰٫۱ در مبنای ده تنها یک رقم معنیدار دارد، اما در نمایش مبنای دو مانتیس آن چندین عدد است که مرتبا تکرار میشوند. یعنی، از هر چند بیت که میخواهید برای ذخیره اعداد استفاده کنید، ۰٫۱ در مبنای دو هرگز با دقت قابل نمایش نخواهد بود.
تفاوت بین جواب محاسبه شده و پاسخ درست معمولا بسیار جزیی است و شاید این خطا را بیاهمیت بشمارید. اما این خطاها میتوانند روی هم انباشته شده و تبعاتی جدی داشته باشند.
پردازشگری که تقسیم بلد نبود
اینتل، پنتیوم که پنجمین نسل پردازندههای x86 بود را در مارس ۱۹۹۳ به بازار عرضه کرد. در نسلهای پیشین، برخی پردازندهها تنها قادر بودند اعمال محاسباتی را روی اعداد صحیح انجام دهند. اما تمامی پنتیومها همگی یک واحد ممیز شناور (FPU) داشتند که قطعهای سختافزاری بود و کار محاسبات ممیز شناور را انجام میداد و باعث شده بود سرعت پردازنده به شدت عالی باشد، چون محاسبات اعشاری روی اغلب پردازندههایی که این واحد را نداشتند باید با استفاده از عملیات اعداد صحیح و به صورت نرمافزاری انجام میشد.
اما این کار در نهایت به زیان اینتل تمام شد. در ژوئن ۱۹۹۴ و کمی پس از آغاز فروش کامپیوترهای مبتنی بر پنتیوم، تامس نایسلی که استاد ریاضی دانشگاه لینچبرگ ویرجینیا بود متوجه شد برنامهای که نوشته در هر بار اجرا جوابهای متفاوتی میدهد.
او همان برنامه را روی ماشینهای مختلف اجرا کرد و متوجه شد مشکل زیر سر پردازنده پنتیوم، و به ویژه دستور FDIV آن است که برای تقسیم اعداد با ممیز شناور به کار میرود. با آنکه این مشکل تنها روی بخشی جزیی از تقسیمهای ممیز شناور تاثیر میگذاشت، اما میتوانست نتایج بدی به همراه داشته باشد. مثلا تقسیم ۴۱۹۵۸۳۵ بر ۳۱۴۵۷۲۷ منجر به جواب ۱٫۳۳۳۷ میشد، در حالی که پاسخ درست ۱٫۳۳۳۸ بود.
FPU پنتیوم از الگوریتم SRT برای تقسیم اعداد ممیز شناور استفاده میکرد. هر چند روشهای سادهتر و روشنتری هم برای تقسیم اعداد وجود دارد، اما الگوریتم SRT سرعت بسیار بالاتری نسبت به سایر روشها داشت. عملکرد SRT به زبان ساده به این ترتیب بود که در یک جدول به دنبال یک سری مقادیر میگشت. این جدول حدود ۱۰۰۰ خانه داشت، اما به دلیل خطای تولید پنج خانه آن پر نشده بود.
با آنکه اندری گرو، مدیر اجرایی اینتل بر این باور بود که این مشکل یک کاربر معمولی را هر ۲۷ هزار سال یکبار به دردسر میاندازد، اما تخمین IBM بسیار بالاتر از اینتل بود: یک مشکل به ازای هر ۲۴ روز.
در نهایت اینتل تصمیم گرفت پردازندههای تولید شده را از بازار جمع کرده و آنها را با پردازندههای بهتر جایگزین نماید، پیشنهادی که مورد استقبال چندانی هم قرار نگرفت. با این حال باعث شد کاربران کامپیوتر برای اینتل لطیفه بسازند؛ مانند این: میدانید چند طراح پنتیوم برای عوض کردن یک لامپ لازم است؟ پاسخ: ۱٫۹۹۹۰۴۲۷۴۰۱۷ نفر!
در خطاهایی که تاکنون دیدهایم مشکل این بوده که اعداد در مانتیس جا نمیگرفتهاند. اما با توجه به طیف بسیار گسترده اعدادی که میتوانند در قالب ممیز شناور جا بگیرند، احتمال این خطاها بسیار کم است.
اما هنگامی که صحبت از اعداد صحیح میکنیم، اوضاع میتواند وخیمتر شود. یک متغیر صحیح ۶۴ بیتی حداکثر قادر به ذخیره عدد ۹,۲۲۳,۳۷۲,۰۳۶,۸۵۴,۷۷۵,۸۰۷ است. اگر به این عدد ۱ اضافه کنید، دچار سرریز (Overflow) شده و مقدار ۹,۲۲۳,۳۷۲,۰۳۶,۸۵۴,۷۷۵,۸۰۸- را به ما میدهد (به منفی پشت عدد دقت کنید). اتفاقی کاملا مشابه در اولین پرواز موشک آریان ۵ آژانس فضایی اروپا روی داد.
البته آن رویداد حتی سادهتر از این بود و تنها شامل کپی کردن یک عدد ذخیره شده در قالب ممیز شناور به محلی برای یک عدد صحیح بود. این محل ۱۶ بیت جا داشت و حداکثر عدد ۳۲۷۶۷ را میتوانست ذخیره کند. البته عدد اصلی بزرگتر از این بود و در نتیجه سرریز روی داد. این خطا مشکلات دیگر را در پی داشت و به طور خلاصه بگوییم: در نهایت آرین ۵ یکی از گرانترین آتشبازیهای تاریخ دنیا شد (شکل ۳).

شکل ۳: موشک آرین ۵ قبل از انفجار در هوا
احتمالا از خود پرسیدهاید آیا کامپیوترهای آینده این مشکلات را برطرف میکنند یا نه. اما جالب است بدانید اغلب خطاهایی که به آنها اشاره کردیم، به جز مشکل سختافزاری اینتل همه قابل پیشگیری بودهاند و عملا خطاهایی نرمافزاری به شمار میرفتهاند.
مثلا خطای سرریز موشک آرین ۵ در اصل خطا نیست، چون پردازنده قرار بوده به این سبک کار کند. هر گاه سرریز روی میدهد، پردازنده Flag مربوط به آن را ۱ میکند تا برنامه متوجه شود.
اما برنامهنویسان آرین ۵ جایی برای بررسی Flag سرریز در برنامه در نظر نگرفته بودند و اگر این کار را میکردند، میتوانستند اقدامات تصحیحی لازم را انجام دهند. به این ترتیب، برنامهنویسان باید مراقب خطاها باشند، هر چند که این کار به کاهش سرعت برنامه میانجامد.
در هر صورت، نتیجه برخی از تقسیمها هرگز به صورت دقیق ذخیره نخواهد شد. دیدیم که یک تقسیم بر ۱۰ رشتهای نامتناهی در مبنای ۲ است. اما در مبنای ۱۰ هم با مشکلات مشابه برخورد داشتهایم؛ مثلا یک تقسیم بر ۳ مساوی میشود با …۰٫۳۳۳۳ تا بینهایت.
میتوان از روشهای مختلفی برای حل مشکل استفاده کرد، مثلا جواب برخی عبارتهای مشکلساز را به صورت مجزا ذخیره کرد تا در صورت لزوم از آنها استفاده شود. درست است که کامپیوترها در انجام کارهای ریاضی ناتوان هستند، اما همیشه راهی برای حل این نقاط ضعف آنها وجود دارد. بنابراین بهتر است بگوییم برنامهنویسان در انجام کارهای ریاضی ناتوان هستند؛ اگر همه آنها نه، حداقل بعضی از آنها!
منبع:computernews.ir
 نیاکان پردازش از ۱۳۷۰ تـــــــا امروز خدمات تکنولوژی اطلاعات و ارتباطات
نیاکان پردازش از ۱۳۷۰ تـــــــا امروز خدمات تکنولوژی اطلاعات و ارتباطات

